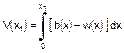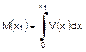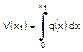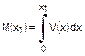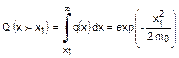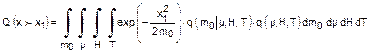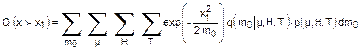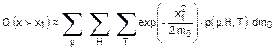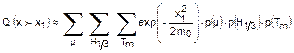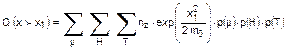|
· · Architettura Navale · Robustezza della Nave · · CARICHI STRUTTURALI DELLA NAVE · Alberto Albert · · CLASSIFICAZIONE
DEI CARICHI · Carico
statico su una nave galleggiante in acqua tranquilla · Carichi
indotti dalle onde · Valutazione
deterministica dei carichi indotti dalle onde
· Distribuzione
trasversale dei carichi d’onda · Carichi
dell'onda sulle piattaforme “off-shore” · Valutazione
probabilistica dei carichi indotti dalle onde in stati di maRE confuso · Valutazioni
dei carichi a breve termine in stati di mare confuso
· Valori
estremi a lungo termine · Estrapolazione
dei valori estremi osservati
· CARICHI DINAMICI Classificazione
dei carichi È
conveniente dividere i carichi che agiscono sulla struttura della nave in
quattro categorie, come esposto di seguito, dove le categorie sono definite
in parte sulla natura del carico ed in parte sulla natura della risposta
della nave: -
carichi statici -
carichi dinamici a bassa frequenza -
carichi dinamici ad alta frequenza -
carichi d’urto Carichi statici I
carichi statici sono carichi che cambiano soltanto quando cambia il peso
totale della nave, come conseguenza della caricazione o della scaricazione, del
consumo di combustibile, o per la modifica della nave stessa: 1)
peso della nave e del relativo contenuto. 2)
spinta statica della nave a riposo od in movimento. 3)
carichi termici derivanti da gradienti di temperatura non lineari all'interno
dello scafo. 4)
carichi concentrati causati dallo stoccaggio in bacino o da arenamento. Carichi dinamici a bassa
frequenza I
carichi dinamici a bassa frequenza sono carichi che variano nel tempo con
periodi che vanno da alcuni secondi a parecchi minuti e quindi si presentano
a frequenze che sono sufficiente basse se confrontate con le frequenze delle
risposte di vibrazione dello scafo e dei suoi componenti. Non c’è
amplificazione in risonanza apprezzabile delle tensioni indotte nella
struttura. I carichi sono denominati dinamici perché hanno origine
pricipalmente dall'azione delle onde per mezzo delle quali la nave si muove
e, quindi, cambiano sempre con il tempo. Possono essere analizzati nei
seguenti componenti: 1)
variazioni di pressione sullo scafo indotte dalle onde. 2)
variazioni di pressione sullo scafo causate dai movimenti oscillatori della
nave. 3)
reazioni inerziali risultanti dall'accelerazione della massa della nave e del
relativo contenuto. Carichi dinamici ad alta
frequenza I
carichi dinamici ad alta frequenza sono carichi variabili nel tempo con
frequenze sufficientemente alte che possono indurre risposta di risonanza
nella struttura della nave. Alcuni dei carichi eccitanti possono essere
abbastanza piccoli nella grandezza ma, come conseguenza dell'amplificazione
in risonanza, possono provocare grandi sforzi e deformazioni. Gli esempi di
tali carichi dinamici sono i seguenti: 1)
carichi idrodinamici indotti dagli apparati di propulsione sullo scafo o
sulle appendici 2)
carichi comunicati allo scafo da macchinari rotanti sbilanciati o
contrapposti 3)
carichi idroelastici causati dall’interazione delle appendici con il flusso
fluido di poppa 4)
carichi indotti dalle onde dovuti essenzialmente alle onde corte la cui
frequenza d’incontro coincide con la frequenza naturale più bassa dello scafo
e che, quindi, possono eccitare un’apprezzabile risposta di risonanza,
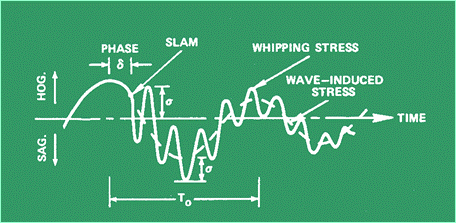
chiamata “springing”. Carichi d’urto I
carichi d’urto sono carichi che derivano dallo sbattimento della prua o dall’urto d’onda sul fondo, sulle
sovrastrutture di prua o su altre parti della struttura dello scafo, compresi
gli effetti per l’acqua imbarcata sulla coperta “green water”. In una nave
miltare, gli effetti delle armi costituiscono una categoria molto importante
di carichi d’urto. I carichi d’urto possono indurre vibrazioni transitorie
dello scafo chiamate “whipping”. Le
più importanti categorie dei carichi sono i carichi statici derivanti dal
peso e dalla spinta della nave (categorie 1) e 2)), ed i carichi dinamici a
bassa frequenza (categorie 1), 2) e 3)). Nelle sezioni seguenti, l'attenzione
sarà dedicata pricipalmente sui metodi correntemente in uso per la
determinazione di questi carichi, con la breve discussione sui carichi
d’urto, d), e sui carichi dinamici ad alta frequenza “springing”, 4), che
sono solitamente considerati importanti in navi flessibili e molto lunghe. Oltre
alle suddette categorie, ci possono essere carichi operativi speciali, che
parte o tutta la struttura può essere invitata a sostenere, e che possono
essere i carichi dominanti per alcune navi. Questi carichi, che possono
essere statici o dinamici, non sono stati considerati in questa discussione.
Alcuni esempi sono: -
carico dovuto al ghiaccio nel caso di una imbarcazione destinata a rompere il
ghiaccio o alla navigazione artica -
carichi causati dall’urto con altre imbarcazioni, pontili o altri ostacoli,
come nel caso di rimorchiatori o pontoni -
impatto dell'apparecchiatura di maneggio del carico, quali le gru a benna o le
coperture delle boccaporte utilizzate nello scarico dei prodotti all'ingrosso -
carichi termici strutturali imposti da carichi speciali trasportati alla
temperatura o alla pressione differenti da quella ambientale -
carichi di sbattimento o d’urto sulle strutture interne causate dal movimento
dei liquidi nelle casse -
atterraggio di velivoli od elicotteri -
carichi accidentali causati da collisione o arenamento. Come
può essere dedotto dalle descrizioni sommarie presentate innanzi, alcuni di
questi carichi possono essere importanti per tutte le navi ed altri carichi
possono essere incontrati soltanto in navi specializzate od in particolari
circostanze. Carico
statico su una nave galleggiante in acqua tranquilla I
carichi statici che agiscono su una nave galleggiante in acqua tranquilla
consistono di due componenti: forze di spinta e forze di gravità, o pesi. La
spinta è la risultante della distribuzione delle pressioni idrostatiche sulla
superficie esterna ed immersa della
nave. Questa pressione è una forza di superficie la cui direzione è sempre
normale allo scafo. La forza di spinta è, quindi, la risultante
perpendicolare alla superficie dell'acqua ed diretta verso l'alto. I pesi
sono le forze delle masse distribuite della nave e dei suoi contenuti ed il
senso di tali forze peso è sempre verticale verso il basso. Questo sistema di
componenti delle forze agenti è illustrato schematicamente nella Figura 1.
Figura 1 Se
integriamo le pressioni locali di spinta lungo un'unità di lunghezza intorno
ad una sezione trasversale in una data posizione longitudinale, la risultante
è una forza verticale di spinta per unità di lunghezza la cui intensità è
data da ρ*g*A dove ρ*g è la densità di peso dell’acqua (ρ è la
densità di massa, o massa per unità di volume) ed A è l‘area della sezione
immersa. Similmente, possiamo sommare insieme tutti i pesi contenuti in
un’unità di lunghezza della nave, nella stessa sezione già considerata,
ottenendo un peso totale per unità di lunghezza. Il peso strutturale netto
per unità di lunghezza è la somma algebrica della spinta e del peso per unità
di lunghezza. Per convenienza, quando sono usate le unità S.I. tutti i carichi
– sia di spinta che di peso - possono essere espressi in termini di massa. I
carichi individuali possono avere effetti strutturali sia locali che globali.
Un macchinario molto pesante induce carichi localizzati molto intensi nei
relativi punti di connessione alla nave e le sue fondazioni possono essere
progettate per distribuire anche questi carichi nella struttura dello scafo.
Allo stesso tempo, il peso di questo macchinario contribuisce alla
distribuzione delle forze di taglio e dei momenti flettenti agendo in tutte
le posizioni lungo lo scafo. Se una parte del contenuto della nave è composto
dai liquidi, per esempio combustibile o carico liquido, là ci saranno forze
idrostatiche di pressione esercitate da tali liquidi e che saranno normali
alle superfici perimetrali delle casse entro le quali questi saranno
contenuti. Questi carichi di pressione interni possono avere importanti
effetti strutturali locali e devono essere considerati quando si progettano
le paratie e gli elementi di confinamento delle casse. La
disposizione geometrica e l’andamento risultante sia dello stato tensionale
che flessionale di una tipica struttura navale sono tali che è solitamente
conveniente dividere la struttura e la relativa risposta in tre componenti,
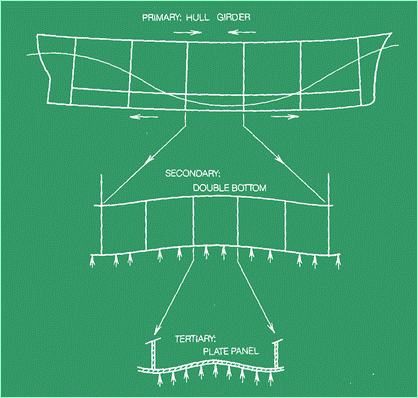
che sono identificati come primari, secondari e terziari (Figura. 2).
Figura 2 Tali
componenti sono descritte come segue: - risposta
primaria è la risposta dell’intero scafo quando si flette e si torce come una
trave, sotto la distribuzione longitudinale esterna dei carichi verticali,
laterali e di torsione. -
risposta secondaria comprende gli sforzi e le deformazioni di un singolo
pannello irrigidito da profilati, per esempio il pannello della struttura del
fondo contenuto fra due paratie trasversali adiacenti. Il carico del pannello
è normale al suo piano ed i contorni del pannello secondario sono costituiti
solitamente da altri pannelli secondari ( fasciame del fianco e paratie). -
risposta terziaria descrive le deformazioni fuori dal piano e lo stato
tensionale associato di un singolo pannello del fasciame. Il carico è normale
al pannello ed i relativi appoggi sono costituiti dai rinforzi del pannello
secondario di cui è parte integrante. Dalla
suddetta descrizione si vede che è necessario a volte conoscere la
distribuzione localizzata dei carichi ed in altri casi, a seconda dalla
risposta strutturale che si è cercata, conoscere la distribuzione della
risultante dei carichi locali ( per esempio il carico per unità di lunghezza
dell'intero scafo ). L'analisi
della risposta primaria è effettuata ipotizzando che l'intero scafo della
nave si comporti come una trave il cui carico è dato dalla distribuzione
longitudinale dei pesi e della spinta sullo scafo. Come in qualsiasi calcolo
di resistenza di una trave, è dapprima necessario integrare i carichi per
ottenere la distribuzione longitudinale della forza di taglio complessiva ed
integrarla ancora per ottenere il momento flettente. I carichi in acqua
tranquilla contribuiscono per una buona parte del taglio totale e del momento
flettente di molte navi, ai quali devono essere aggiunti successivamente gli
effetti indotti dalle onde. La Figura 3 illustra una tipica distribuzione
longitudinale di peso e di spinta per una nave galleggiante in acqua
tranquilla.
Figura 3 Nella
parte più inferiore di questa figura è tracciata una curva (1) della forza di
spinta per unità di lunghezza, che come notato precedentemente è uguale alla
densità di peso, ρ*g, dell’acqua per l’area della sezione. La curva
superiore (2) in questa figura mostra la distribuzione longitudinale della
forza peso tracciata secondo la convenzione comunemente impiegata. In questa
procedura, la lunghezza della nave è divisa in un certo numero di spazi uguali,
per esempio nelle venti o più suddivisioni che sono state usate nella
preparazione del piano di costruzione delle linee d’acqua. Tutti i pesi dello
scafo, delle attrezzature e dei contenuti che si trovano nell'intervallo fra
la stazione i e la stazione i+1 sono sommati e trattati come un singolo
carico uniformemente distribuito sopra questo intervallo di suddivisione
longitudinale. Ciò è essenzialmente un processo di conteggio in cui ogni
elemento nella nave [ per esempio, la struttura dello scafo (fasciame,
ossature, materiale di saldatura), l’allestimento (condotte, copertura del
ponte, movimentazione del carico), l’apparato di propulsione, il carico ed
altro ] è registrato ed assegnato ad un intervallo della suddivisione. La
procedura deve essere sviluppata con cura meticolosa ed in grande dettaglio
così da assicurare un’adeguata accuratezza. Come nel caso della maggior parte
dei calcoli ripetitivi anche questa procedura si presta facilmente per essere
effettuata con elaboratori elettronici. L’ipotesi
di una distribuzione dei pesi, che è assunta in questo stadio uniforme negli
intervalli della distribuzione, è soltanto un'approssimazione della
distribuzione reale del peso. Alcuni elementi del peso si presenteranno come
pesi quasi concentrati in questa distribuzione longitudinale. Per esempio, il
peso di una paratia trasversale sarà, in realtà, distribuita
longitudinalmente su una porzione molto breve della lunghezza della nave
uguale allo spessore del fasciame della paratia. I pesi di determinati elementi
quali i grandi componenti dell’apparato di macchina (turbine, motori diesel)
possono essere trasmessi alla struttura della nave come carichi puntuali
nelle posizioni dei tirafondi di fondazione. Similmente, i “containers” sono
sostenuti solitamente sui supporti posizionati sotto i loro angoli ed il loro
peso totale è trasmesso alla struttura dello scafo con carichi puntuali in
queste posizioni. La vera distribuzione dei pesi sarà quindi un grafico molto
più irregolare di quello che è indicato nella Figura 3 e consisterà di alcuni
pesi distribuiti e di alcuni pesi concentrati. Può essere evidenziato,
tuttavia, che le integrazioni che sono realizzate per ottenere dai carichi le
distribuzioni del taglio e poi del momento flettente tendono ad attenuare gli
effetti di queste irregolarità locali. Di conseguenza tutta la distribuzione
ragionevolmente esatta dei carichi, che mantiene il valore corretto della
forza entro un intervallo locale e piccolo confrontato alla lunghezza totale
della nave, condurrà generalmente alle distribuzioni corrette del taglio e
del momento flettente entro limiti
accettabili d'errore. Tuttavia, effetti strutturali localizzati, causati da
notevoli carichi puntuali e particolarmente da elementi pesanti possono
essere analizzati separatamente ed i loro effetti sovrapposti agli effetti
dei carichi restanti. Avendo determinato le distribuzioni dei pesi e delle
spinte, la curva netta del carico (3) è la differenza fra i due. Questa è
tracciata come la terza curva nella Figura 3, con spinta positiva verso
l'alto. Gli stati d’equi1ibrio statico richiedono che il peso totale e la
spinta siano uguali e che il centro di spinta sia sulla stessa linea
verticale del centro di gravità. In termini di curva del carico, questo
richiede che l’integrale di tutto il carico sulla lunghezza della nave e
l’integrale del momento longitudinale del carico siano entrambi nulli. Come
in qualsiasi calcolo a trave, la forza di taglio in una posizione x, uguale a
V(x), è ottenuta come l'integrale della curva del carico ed è tracciata come
la quarta curva di Figura 3
dove: b(x)
= spinta per unità di lunghezza w(x)
= peso per unità di lunghezza Il
momento flettente nella posizione x1, M(x1), è
l’integrale della curva del taglio ed è tracciato come la quinta curva nella
Figura 3:
Nella
parte inferiore della Figura 3 è indicato l'andamento del momento flettente e
del taglio, insieme alle loro convenzioni del segno. Se
consideriamo una data posizione longitudinale, x1, la forza di
taglio è la forza ascendente che la parte sinistra dello scafo esercita sulla
parte destra di questa posizione. Similmente, il momento flettente è il
momento risultante esercitato dalla parte sinistra sulla parte della nave
alla destra della posizione x1. Per essere soddisfatta la
condizione d’equilibrio statico la forza di taglio ed il momento flettente
dovranno essere uguali a zero ad entrambe le estremità della nave. Nell'esecuzione
pratica del calcolo dei carichi in acqua tranquilla oggi sono utilizzati
codici di calcolo per elaboratore elettronico. I programmi disponibili,
contengono i moduli per l'effettuazione dei calcoli quali le proprietà
idrostatiche, la stabilità statica, l’allagamento e la compartimentazione.
L'operazione principale che deve affrontare l'architetto navale consiste
nella redazione e nel controllo dei dati di ipotesi e nella valutazione dei
risultati del calcolo. L'importanza d’ipotesi complete ed esatte deve avere
la giusta enfasi e può essere immediatamente compreso che la compilazione dei
dati completi del peso richiesti per il calcolo del momento flettente e del
taglio nella fase di progetto finale non è un'operazione insignificante. Concludendo
questo paragrafo, dovrebbe essere osservato che il carico statico deve essere
calcolato solitamente per varie distribuzioni di carico considerando anche
altri eventuali pesi variabili presenti per ottenere i valori estremi del
momento flettente e del taglio. Il carico statico deve inoltre essere
combinato con altri eventuali carichi presenti su cui basare il progetto
degli elementi della struttura. Ancora, deve essere considerato che il carico
statico cambierà durante il corso di singolo viaggio per il consumo del
combustibile, per la zavorra che verrà spostata e per il carico che è
caricato e scaricato nei porti di scalo. Una
storia temporale dei cambiamenti nelle tensioni statiche in mezzeria durante
il corso di un lungo viaggio di grande cisterna è stata presentata nella
Figura 4.
Figura 4 Anche
se questa figura mostra le variazioni di sforzo dovuto alle onde e agli
effetti termici, le grandi variazioni nelle linee a tratto spesso sono i
risultati dei cambiamenti nelle quantità e nella posizione dell'acqua salata
nelle casse di zavorra. Le variazioni registrate nelle tensioni in acqua
tranquilla, a parte la temperatura e gli effetti dell'onda, variano da circa
27.6 MPa di trazione a circa 48.3 MPa di compressione. Carichi
indotti dalle onde I principali
carichi indotti dalle onde sono quelli precedentemente citati come carichi
dinamici di frequenza bassa o carichi che coinvolgono i movimenti dell'onda e
della nave e che provocano trascurabile amplificazione dinamica delle
tensioni. Una volta che questi carichi quasi statici sono determinati, la
risposta strutturale in termini di sforzo o deformazione può essere computata
con i metodi d’analisi strutturale statica. Almeno
quattro procedure con vari gradi di sofisticazione possono essere utilizzate
nella valutazione dei carichi indotti dalle onde e dei momenti flettenti
risultanti oltre che delle forze di taglio: -
metodi approssimati -
misure di deformazione e o di pressione sulle navi esistenti -
misure in laboratorio dei carichi sui modelli - calcolo
diretto dei carichi idrodinamici indotti dalle onde Metodi approssimati Nel
processo preliminare di progetto è spesso desiderabile effettuare una
valutazione preliminare del carico strutturale dello scafo con metodi approssimati,
a volte prima che siano state elaborate informazioni dettagliate riguardo
alla distribuzione del peso o delle linee dello scafo. Sono disponibili
metodi approssimati che includono formulazioni semi-empiriche e calcoli
quasi-statici. I
primi testi di architettura navale contengono le descrizioni di una procedura
per cui la nave è immaginata in uno stato di equilibrio statico o sulla
cresta o sul cavo di un'onda la cui lunghezza è uguale a quella della nave,
L, e l’altezza pari ad L/20. Usando la distribuzione longitudinale della
spinta per un tale profilo dell'onda e una distribuzione ipotetica del peso,
possono essere calcolate le curve della distribuzione longitudinale della
forza di taglio e del momento flettente, solo come se si fosse in acqua
tranquilla. Gli esperimenti ed i metodi di calcolo più esatti hanno indicato
che questa procedura altamente semplificata sopravvaluta con un notevole
margine il momento flettente indotto dall’onda per qualsiasi altezza d'onda
data; questo è conseguenza del fatto che vengono trascurati gli effetti
dinamici ed idrodinamici connessi con le pressioni dell'onda ed i movimenti
della nave. Tale procedura è utile principalmente quando usata paragonandola
ai dati dei progetti precedenti. La
maggior parte delle società di classificazione ora impiegano una formulazione
semplificata da usare nella valutazione del momento flettente e della forza
di taglio indotti dalle onde da aggiungere al momento ed al taglio in acqua
tranquilla. Tuttavia, le altezze d'onda efficaci usate in queste formulazioni
sono state derivate da analisi dettagliate che includono gli effetti dinamici
ed idrodinamici e, pertanto, non sono soggetti alle limitazioni del calcolo
dell'onda statica appena descritto. Le regole dell’ABS definiscono un momento
flettente dell'onda estrema che, insieme con il momento flettente in acqua
tranquilla e le tensioni ammissibili regolamentari, si intende che debba
essere usato nella determinazione del modulo di resistenza richiesto:
dove: C2
e Kb sono coefficienti tabulati dipendenti dal coefficiente di
blocco L
e B sono, rispettivamente, lunghezza e
larghezza della nave H
è un’altezza d’onda o un coefficiente di momento flettente dipendente da L I
valori dati nei regolamenti per H mostrano una tendenza ascendente graduale
con la lunghezza della nave, stabilizzandosi su un valore costante di 305 m. Tutte
le costanti dell'equazione (3) sono basate su una notevole messe di dati
ottenuti da numerose navi tramite una combinazione di calcoli, di prove su
modello e di misure in grande scala. L'uso di un'altezza d'onda nominale
prende in considerazione la risposta della nave, dipendente dal formato della
nave, congiuntamente alla severità delle onde previste durante la vita della
nave. È stato rilevato che i valori previsti da tale formula sono
perfettamente d'accordo con le previsioni analitiche usando le onde
dell'Atlantico del Nord ed in accordo con altre valutazioni a lungo termine
del momento flettente massimo dell'onda, per navi di proporzioni medie che
formano uno “standard”, non avendo caratteristiche insolite nella geometria o
nella distribuzione longitudinale dei pesi. Poiché tale momento flettente può
essere valutato senza la conoscenza dettagliata della distribuzione del peso
o della geometria dello scafo, risulta utile per le valutazioni preliminari
di progetto. Una volta usato con le tensioni ammissibili adatte fornisce un
calcolo tipico soddisfacente per la robustezza longitudinale anche se basato
su dati empirici per navi convenzionali. I
dettagli dei calcoli tipici per la robustezza longitudinale per la marina
sono classificati, ma è fornita questa dichiarazione generica, "le travi
primarie dello scafo per scafi in acciaio comune sono progettate per un
livello tensionale di 130 MPa sulla singola ampiezza disponendo la nave su
un'onda trocoidale di altezza 1.1*√LBP e lunghezza = LBP" ed
effettuando di seguito un calcolo quasi-statico convenzionale. Misure di deformazione e o di
pressione sulle navi esistenti Le
misure al vero non possono ovviamente essere usate per ottenere dati
specifici per il progetto di una nuova nave. Anche se i risultati di tali
misure si applicano soltanto alle specifiche navi studiate, sono di grande
utilità per verificare i metodi di previsione basati sulle leggi della
probabilità che saranno descritti più avanti. Le misure al vero soffrono di
un grosso svantaggio, oltre a quello della spesa, che è la difficoltà nel
misurare con accuratezza l'ambiente marino per la correlazione con i carichi
misurati. Mentre tentativi numerosi sono stati fatti per sviluppare boe
economiche o strumenti navali per misurare le onde, uno strumento
completamente soddisfacente ancora non è stato realizzato. Il valore
principale delle misure di risposta al vero ai carichi (sollecitazione o
deformazione), si trova quindi nello sviluppo delle previsioni statistiche a
lungo termine dei carichi sullo scafo indotti dalla navigazione e nelle
misure effettuate durante un periodo pluriannuale. Poiché queste previsioni
possono essere collegate con più dati climatologici di lunga durata
dell'onda, il problema della misura dell'onda nelle vicinanze immediate della
nave è di minore importanza. Continue
sono le misure al vero ed a lungo termine su navi di vari tipi e formati
effettuate da parecchi enti di classificazione marittima ed organismi di
ricerca intorno al mondo e le descrizioni di tali lavori possono essere
trovate agevolmente in letteratura. Queste misure a lungo termine ed al vero
sono utilizzate quindi per verificare le previsioni teoriche. Misure in laboratorio dei
carichi sui modelli In
questa procedura, un modello geometricamente e dinamicamente simile alla nave
è equipaggiato con strumenti che misurano il taglio verticale e orizzontale
oltre al momento flettente, o al momento di torsione, al centro nave ed in
altre sezioni. Ciò può essere compiuto registrando le forze o le deformazioni
fra parecchi segmenti prodotti da tagli trasversali nel modello. Anche i
carichi impulsivi possono essere determinati registrando le pressioni in
parecchi punti distribuiti sopra la superficie del modello. Gli esperimenti
sono eseguiti in vasche di rimorchio equipaggiate per produrre sia onde
normali che casuali. La vasche più versatili sono larghe rispetto alla loro
lunghezza ed il modello può, quindi, essere esaminato in obliquo così come di
prua e di poppa. I
risultati delle prove su un modello di una cisterna indicano che il momento
flettente longitudinale laterale in mezzeria può avvicinarsi od eccedere il
valore del momento flettente longitudinale verticale quando la nave ha angoli
d’incontro obliqui in onde regolari. Le
prove su modello sono state fatte a 10 nodi di velocità con angoli d’incontro
obliqui rispetto alle onde che hanno una lunghezza effettiva uguale alla
lunghezza del modello. La lunghezza dell'onda era quindi uguale alla
lunghezza del modello per il coseno dell'angolo d’incontro. Un'altezza d'onda
di 1/48 della lunghezza del modello è stata usata per tutte le lunghezze
d’onda per evitare un’eccessiva immersione del modello. È
stato trovato che il momento flettente laterale era abbastanza sensibile al
cambiamento della direzione dell’onda ed all’effettiva lunghezza d’onda. Il
momento flettente aumentava quasi linearmente quando l'angolo d’incontro
variava da 180° a 120°. I momenti massimi alle velocità nulle d’avanzamento
accadono ad un angolo d’incontro di circa 135°. Il ritardo di fase fra il
momento flettente laterale e verticale e dell’ordine del quarto di giro. Dovrebbe
essere considerato ancora che la ripidità effettiva dell'onda aumenta
spostando l’angolo d’incontro dal mare di prua al mare al mascone. Con mare
di prua e lunghezza delle onde di modello si ha un rapporto di 1/48; la
ripidità cambia a 1/24 per lunghezza d’onda efficace ed angolo d’incontro di
120°. La
Figura 5 da Numata mostra il rapporto fra i momenti flettenti longitudinali
verticali e laterali per un angolo d’incontro di 120°, velocità di 10 nodi ed
un rapporto altezza dell'onda lunghezza modello di 1/48, corrispondente ad
un'altezza d'onda al vero di 3.12m.
Figura 5 Le
prove su modello sono state eseguite inoltre in onde irregolari con l'altezza
media delle onde più alte del 10% rispetto ai 7.01m al vero. Per il confronto
con i momenti flettenti verticali in onde normali, i valori nella fig. 5 sono
stati aumentati del rapporto delle altezze d'onda, vale a dire 23/10.5. Il
momento flettente longitudinale laterale e verticale di queste prove su
modello sono approssimativamente della stessa grandezza e non rappresentano
le circostanze peggiori che potrebbero essere incontrate in mare. La nave
Ocean Vulkan, per esempio, ha osservato il momento flettente longitudinale
laterale di grandezza paragonabile al momento verticale in quasi tutti gli
stati di mare. I momenti massimi si sono presentati per angoli d’incontro da
110° a 140°. Il massimo momento è stato di 24.800 t*m, corrispondente ad uno
stato tensionale di 39 MPa e questi momenti erano frequentemente in fase con
i momenti flettenti verticali. Gli
esperimenti iniziali di questo tipo sono stati concepiti per fare luce sulla
natura fondamentale dei carichi d’onda dinamici. Gli esperimenti più recenti
hanno avuto l'obiettivo principale di fornire i dati con i quali calibrare le
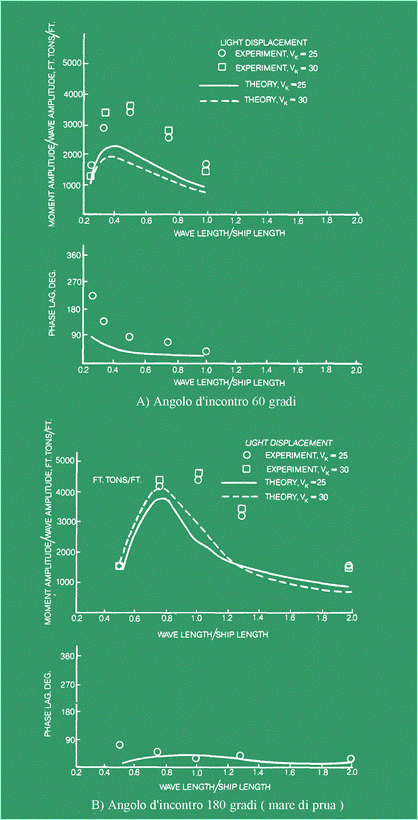
procedure teoriche di calcolo citate nella procedura successiva. Alcuni
confronti tra risultati sperimentali e teorici sono stati rappresentati nella
Figura 6.
Figura 6 Mentre,
in linea di principio, esperimenti di questo tipo potrebbero essere
effettuati per valutare i carichi strutturali nel progetto di una nuova nave,
questo è eseguito raramente a causa del tempo necessario e della relativa
spesa. Inoltre ora sono disponibili un certo numero di codici di calcolo per
elaboratore che offrono la possibilità di studiare una gamma molto più vasta
di stati di carico e di stati di mare di quanti sia possibile verificarne in
un programma di prove su modello e a costi considerevolmente inferiori.
Quindi, l'impiego principale per le prove su modello è quello di fornire i
dati iniziali o verificare le tecniche utilizzate con l’elaboratore. Calcolo diretto dei carichi
idrodinamici indotti dalle onde In
questo paragrafo, sono state analizzate delle appropriate teorie
idrodinamiche adatte per il calcolo dei moti della nave in moto ondoso oltre
che per il calcolo delle forze di pressione causate dalle onde e dal
movimento della nave indotto da quello delle onde. Nella determinazione dei
carichi strutturali le forze che derivano dalla viscosità del fluido
solitamente possono essere trascurate se paragonate alle forze di pressione,
tranne nel caso del rollio. Il carico strutturale totale in ogni istante è
quindi la somma delle forze di pressione dell'onda, delle pressioni indotte
dal movimento della nave e dei carichi di reazione dovuti all'accelerazione
delle masse della nave. Si noti che un passo preliminare nel calcolo della
quota parte dei carichi dipendenti dal movimento è il calcolo della risposta
dei movimenti di corpo rigido della nave causati dalle forze eccitanti del
moto ondoso. Sia l'analisi delle forze idrodinamiche che il calcolo della
risposta dei movimenti saranno discusse in un successivi paragrafo.
L'applicazione di queste tecniche al calcolo delle forze di taglio e del
momento flettente indotti dalle onde regolari è stata descritta nel paragrafo
seguente. E’ stato inoltre mostrato che i risultati in onde regolari possono
essere applicati alla previsione delle forze e dei momenti in mari
irregolari. Per ottenere una previsione esatta e puramente analitica del
comportamento strutturale a lungo termine di una nave, la ricerca sta
continuando nelle discipline della idrodinamica pura, dell'analisi delle
tensioni, della fatica dei materiali e nella raccolta delle statistiche di
lunga durata delle onde negli oceani del mondo. Valutazione
deterministica dei carichi indotti dalle onde Il
calcolo del momento flettente, della forza di taglio e della torsione di uno
scafo in moto ondoso richiede la conoscenza della distribuzione nel tempo
delle forze del fluido sulla superficie bagnata dello scafo (opera viva)
insieme alla distribuzione della distribuzione dei carichi di reazione
inerziali. I carichi fluidi dipendono dal moto dell’acqua indotto dal moto
ondoso e dai corrispondenti movimenti della nave. I carichi inerziali sono
uguali al prodotto delle masse locali della nave e dell’accelerazione
assoluta locale. La forza di taglio ed il momento flettente sono allora
ottenuti in ogni istante valutando il primo ed il secondo integrale della
distribuzione longitudinale delle forze verticali od orizzontali nette per
unità di lunghezza. Le espressioni per questi integrali sono simili a quelle
usate nei casi di acqua tranquilla, equazioni (1) e (2), con il termine di
spinta sostituito dalla forza fluida variabile nel tempo e per unità di
lunghezza ed il termine del peso sostituito dai carichi di reazione inerziali
per unità di lunghezza. I risultati sono da aggiungere a quelli in acqua
tranquilla. Come notato precedentemente, il calcolo dei carichi inerziali ed
una parte dei carichi fluidi richiede che in primo luogo si determinino i
movimenti della nave indotti dalle onde. La
soluzione per il calcolo di questi movimenti ed il sistema dei carichi fluidi
è oggi frequentemente svolta con l'uso di una procedura basata sulla
cosiddetta “strip theory” (teoria della striscia). I particolari della “strip
theory”, compresi i presupposti fondamentali e le limitazioni dei risultati,
sono stati sviluppati dettagliatamente in un paragrafo successivo. Questa
procedura è stata sviluppata in parecchi codici di calcolo per elaboratori
elettronici. I codici di calcolo della “strip theory” sono ora d'uso comune
tra professionisti, le società di classificazione e gli enti governativi
quando le indagini sistematiche di progetto della nave riguardo ai carichi
d’onda oltre all'analisi di situazioni di carichi inusuali cadono fuori della
gamma delle formule e delle procedure semplificate. I risultati predetti
dalla “strip theory” sembrano essere in buon accordo con i risultati sperimentali
dei movimenti verticali di beccheggio e sussulto; ma è osservato solitamente
un grado di correlazione piuttosto basso per i movimenti laterali di
scarroccio, rollio ed imbardata. A queste previsioni di movimento
corrispondono i carichi verticali, i tagli, i momenti flettenti e di torsione
in maniera piuttosto più precisa. Può essere plausibile che la ricerca
continua sulla idrodinamica della nave induca miglioramenti continui nelle
possibilità applicative di tali codici di calcolo. Di seguito sono state
riepilogate le caratteristiche principali della “strip theory” così come è
applicata nella previsione dei carichi strutturali di una nave e si potrà
fare riferimento all’apposito paragrafo per i particolari della teoria nelle
sua applicazioni per gli aspetti più generali nel calcolo del movimento della
nave. Per
semplicità, possono essere considerate soltanto le componenti verticali dei
carichi che agiscono su una nave che procede con onde regolari di prua, come
illustrato nella Figura 7.
Figura 7 Come
conseguenza della simmetria sul piano verticale longitudinale della nave e
delle onde, i movimenti ed i carichi avranno componenti soltanto in questo
piano. In qualsiasi istante, il movimento della nave consisterà di movimenti,
funzioni del tempo, di beccheggio, sussulto ed avanzamento sovrapposti ad una
velocità media di avanzamento, Uo. Uno
dei presupposti fondamentali della “strip theory” lineare è che sia le
ampiezze dei movimenti della nave che delle onde sono, in un certo senso,
piccole. Di conseguenza, è possibile considerare la forza verticale
istantanea totale su una striscia o su un elemento trasversale sottile di
lunghezza, dx, come composta dalla somma di parecchi termini che sono
calcolati indipendentemente l’uno dall’altro. Due di queste forze elementari
sono la spinta dell'acqua ed il peso dell'elemento sui tratti che
costituiscono la lunghezza della nave. Queste sono le stesse forze che
compaiono nelle equazioni (1) e (2) per i carichi in acqua tranquilla cioè il
taglio ed il momento flettente e non occorre considerarli ora. Le forze
restanti, funzioni del tempo, risultano dalle reazioni inerziali e dalle
pressioni dell'acqua che sono associate alle onde ed ai movimenti della nave
indotti dalle onde stesse. Le forze viscose, che sono considerate
relativamente importanti (eccetto per lo smorzamento del rollio), sono
ignorate nel calcolo dei carichi verticali. In questo quadro le forze
verticali dei fluidi sui vari elementi possono essere suddivise, come segue,
in cinque categorie, tutte espresse in unità di forza: a) la componente della forza di pressione dell’onda
calcolata come se la presenza della nave non disturbasse né le onde incidenti
né la distribuzione delle forze dinamiche di quelle onde. Questa è denominata
la forza di Froude-Krylov, b) la componente della forza di pressione dell’onda
calcolata con il sistema delle onde diffratte. Queste onde risultano dalla
riflessione e distorsione delle onde incidenti quando interferiscono con la
nave. Questa forza rappresenta una correzione delle forze di Froude-Krylov
per il disturbo introdotto nel sistema delle onde per la presenza della nave.
c) un termine proporzionale allo spostamento verticale
istantaneo del tratto di scafo dalla relativa posizione media, come se fosse
in acqua tranquilla. Questa è denominata la forza di richiamo idrostatico ed
è uguale al cambiamento nella spinta statica media dell'elemento. d) un termine proporzionale alla velocità verticale
istantanea del tratto di scafo e denominata forza di smorzamento. e) un termine proporzionale all'accelerazione verticale
istantanea del tratto di scafo e denominata forza di massa aggiunta. Le
prime due di queste forze, una volta sommate, contengono la forza totale
eccitante indotta dalle onde e calcolata come se la nave si muovesse
costantemente in avanti attraverso le onde ma non avvertisse alcuna risposta
di movimento oscillatorio in risposta alle forze d'onda. Le ultime tre forze
sono calcolate come se la nave stesse subendo il movimento oscillatorio
indotto dalle onde mentre si muove alla velocità d’avanzamento costante
attraverso l'acqua tranquilla. In aggiunta alle forze da (a) ad (e) qui sopra
descritte, deve essere aggiunta la forza inerziale di reazione di quella
parte della massa (peso / g) della nave che è contenuta nel tratto dx. Se la
massa della nave per unità di lunghezza è denotata m(x), questa forza di
reazione è data, secondo il principio di d'Alembert, da -m(x)*ay*dx,
dove ay è la componente dell'accelerazione assoluta della sezione
x nel senso parallelo all’asse y della nave. Se ora denotiamo la somma delle
cinque componenti fluide delle forze che agiscono sulla striscia, dx, con
f(x)dx, allora la forza totale in qualsiasi istante è la somma delle forze
fluide e della reazione inerziale, q(x)dx, data da
In
qualsiasi istante, la forza di taglio, V(x1), in una sezione ove
la coordinata x è x1 è ottenuto integrando il q(x) dall'estremità
addietro della nave, x = 0, fino alla stazione x = x1. Il momento
flettente alla sezione x1 è ottenuto, a sua volta, integrando la
forza di taglio, V(x), da x = 0 ad x = x1:
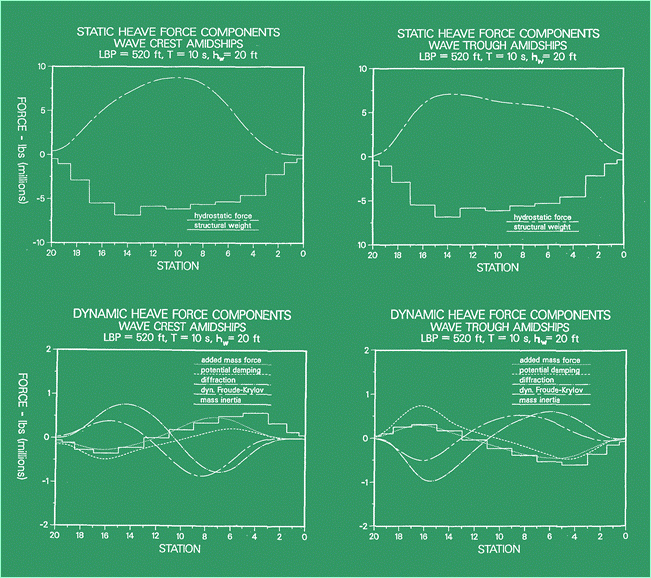
La
Figura 8 illustra i differenti componenti della distribuzione di carico in un
certo istante per una nave che ad esempio si muove in un'onda sinusoidale
semplice di ampiezza unitaria.
Figura 8 In
questa figura si nota che il carico totale consiste di un certo numero di
componenti di grandezza in qualche modo simile che possono differire sia nel
segno che nella fase. Ci può essere annullamento o rinforzo fra i differenti
componenti, con il risultato che il carico totale può essere più grande o più
piccolo di ogni componente isolato. Questo annullamento o rinforzo varia
sulla lunghezza della nave ed inoltre varia con la frequenza d'incontro
dell'onda. Nella
discussione precedente sulla forza su una sezione della nave, è stata
descritta una procedura in cui la forza totale si suddivide in parecchi
componenti, ciascuno dei quali può essere calcolato indipendentemente dagli
altri. Su questa assunzione di linearità è basata la “strip theory”, ed è
possibile quindi calcolare il taglio ed il momento flettente in onde regolari
di qualsiasi ampiezza e frequenza desiderata. La maggior parte dei codici di
calcolo dei movimenti della nave contengono un modulo per effettuare questo
calcolo a differenti angoli di incontro delle onde come per il caso del mare
di prua appena discusso. È
indicato nel capitolo apposito sulla “strip theory” che la componente della
forza d'onda regolare dipende dalla frequenza dell'onda, dalla forma dello
scafo, dalla velocità della nave e dall’angolo d’incontro. I coefficienti
idrodinamici di smorzamento e di massa aggiunta dipendono dalla forma dello
scafo, dalla velocità della nave e dalle frequenze d’incontro delle onde. Le
forze d'onda agiscono sulla nave ad una frequenza uguale alla frequenza
d’incontro e, come conseguenza della rappresentazione lineare dei movimenti
di risposta della nave, i movimenti ed i carichi correlati ai movimenti si
presenteranno a questa stessa frequenza. In generale, ogni movimento o
risposta variabile dei carichi può essere divisa in una componente in fase
con le onde incontrate ed in una componente in contrapposizione di fase
(quadratura) con le onde. Si vede, quindi, che i componenti dei carichi
strutturali q(x), V(x) ed M(x) in una posizione specifica, x, lungo la nave,
sono quantità variabili sinusoidalmente la cui frequenza è uguale alla
frequenza d'incontro dell'onda e, l'ampiezza e la fase variano con la
frequenza. Quando
consideriamo una nave che naviga attraverso un realistico mare irregolare è
una fortuna che la linearità si applichi anche se approssimativamente nella
descrizione dello stato di mare. Lo stato di mare può essere suddiviso in un
numero teoricamente infinito di componenti d'onda di varie ampiezze,
frequenze (lunghezze) e direzioni. Data l’assunzione di linearità della
risposta del carico della nave dove qualsiasi componente d'onda regolare può
essere assunto come direttamente proporzionale all'ampiezza di quell'onda,
allora la risposta della nave in mare confuso può essere calcolata come la
sovrapposizione lineare delle risposte ai vari componenti presenti nel moto
ondoso. Di conseguenza, i calcoli dei componenti della forza, del movimento e
del carico sono inizialmente effettuati per una serie di componenti
elementari di onde regolari ciascuno di ampiezza unitaria e frequenza uguale
ad uno dei componenti dello stato di mare confuso. Le risposte unitarie
risultanti sono successivamente moltiplicate per le ampiezze reali delle onde
componenti lo stato di mare e sono sommate insieme per ottenere lo spettro di
risposta corrispondente allo stato di mare reale. Questo processo di
sovrapposizione lineare costituisce virtualmente la base per tutti i calcoli
delle risposte della nave a tutti gli stati di mare casuali e realistici ed i
particolari possono essere trovati nel capitolo dedicato a questo argomento,
compreso un esempio di calcolo del momento flettente dell'onda. I risultati
sono sotto forma di valori rms del taglio e del momento flettente, dai quali
possono essere derivate le proprietà statistiche a breve termine della
risposta e l'estensione al calcolo dei carichi estremi da prevedere durante
la vita della nave è discussa nei paragrafi successivi. Se,
durante la propria vita, la nave opera in varie condizioni di distribuzione
di carico ed immersione, ci saranno diversi gruppi di funzioni q(x), V(x) ed
M(x) associati ad ogni caricazione. Affinché l'architetto navale possa
progettare il caricamento strutturale più severo che la nave possa avvertire
durante il corso della vita della nave, i calcoli di “strip theory” devono
essere effettuati per la gamma completa di frequenze, di altezze d'onda e di
angoli d’incontro attesi. Questi calcoli devono essere ripetuti per tutte le
combinazioni di velocità e condizioni di carico alle quali la nave opererà.
Molti dei codici di calcolo disponibili e destinati agli elaboratori
contengono i mezzi per l’effettuazione dei calcoli multipli in modo facile ed
efficiente. I più specializzati di questi contengono inoltre le disposizioni
per l'effettuazione della sovrapposizione che conduce alla risposta in mare
confuso, insieme all'analisi probabilistica che conduce alle valutazioni dei
movimenti e dei carichi estremi. Distribuzione
trasversale dei carichi d’onda Per
potere calcolare la risposta secondaria o terziaria dei componenti
strutturali quali i pannelli di fasciame irrigiditi o meno è necessario
conoscere la distribuzione dei carichi di pressione del fluido e
d’accelerazione sulla superficie del pannello. Allo scopo di analizzare la
robustezza trasversale, è quindi richiesta la distribuzione dei carichi
trasversali intorno alla sezione della nave. Si noti che la forza sezionale
per unità di lunghezza usata nel calcolo del taglio longitudinale e del
momento flettente nel paragrafo precedente è la risultante o l'integrale di
questo carico distribuito intorno alla sezione. Un calcolo dell'onda e della
distribuzione di pressione indotta dai movimenti della nave è dato da Kim ed
alcuni dei suoi risultati sono indicati in Figura 9.
Figura 9 I
due diagrammi mostrati in questa figura danno l'ampiezza (ma non la fase)
della variazione di pressione dinamica intorno alla sezione di mezzeria e
questo include gli effetti sia dei movimenti dell'onda che della nave. Può
essere notato che le pressioni nell'onda sopra la linea di galleggiamento in
acqua tranquilla non sono state ottenute, poiché la teoria idrodinamica
lineare calcola la forza dei fluidi soltanto sulla parte immersa media della
nave. La pressione su questa zona deve quindi essere valutata separatamente. La
variazione di pressione dinamica più grande è stata trovata in tutti i casi
vicino al galleggiamento e nei mari di prua o al traverso; l'ampiezza è più
grande sul fianco che si affaccia verso le onde in arrivo. L'ampiezza più
bassa di tale variazione di pressione si trova nelle vicinanze della chiglia,
che, tuttavia, deve sopportare la più alta pressione statica. I codici di
calcolo più completi per i movimenti della nave usati per il calcolo del
taglio e del momento flettente indotti dal moto ondoso forniscono inoltre la
distribuzione di pressione sopra la superficie dello scafo. Carichi
dell'onda sulle piattaforme “off-shore” Molte
piattaforme “off-shore” di perforarazione o per la produzione di idrocarburi
sono decisamente diverse nella forma geometrica dalle usuali forme di scafo
navali, ma si approssimano molto bene come telai strutturali di elementi
tubolari snelli. L'analisi strutturale di tali piattaforme è effettuata
approssimativamente con i metodi d’analisi strutturale tridimensionale ed i
carichi applicabili richiedono metodi di calcolo adatti alla geometria della
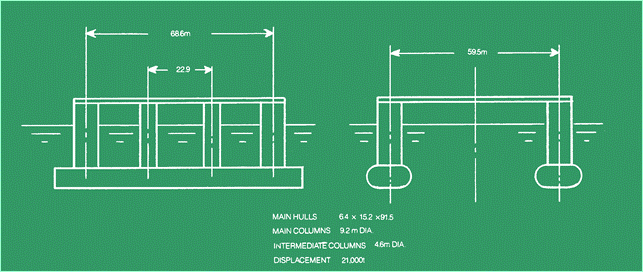
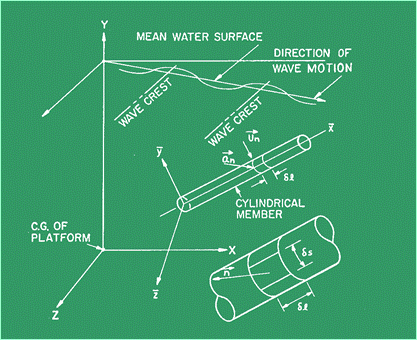
struttura. Una tipica piattaforma è illustrata nella Figura 10.
Figura 10 Una
valutazione ragionevolmente buona delle forze d'onda può essere ottenuta
calcolando la forza su ogni membro come se non ci fosse interferenza
idrodinamica fra i membri adiacenti ed il membro in questione quando siano
stati esposti al campo di flusso dovuto alla combinazione delle onde e del
movimento della piattaforma. Usando una formula proposta per primo da Morison
la forza su un membro, è illustrata nella Figura 11
Figura
11 mentre
la forza per unità di lunghezza, l, può essere approssimata a:
dove: p
=pressione del fluido calcolata sulla superficie dell’elemento come se questo
non disturbasse il flusso n
= vettore normale esterno all’elemento D
= diametro dell’elemento CD
= coefficiente di resistenza CM
= coefficiente di massa aggiunta Un
= risultante normale della velocità in mezzeria an
= risultante normale della accelerazione in mezzeria ds
= porzione di lunghezza dell'arco di circonferenza dell’elemento Con
l'applicazione del metodo di linearizzazione equivalente, il termine
quadratico della forza di resistenza può essere sostituito da una forza di
resistenza lineare. L'analisi risultante per i movimenti ed il carico
strutturale di una piattaforma ora diventa lineare ed i principii della
decomposizione e della combinazione del carico che precedentemente sono stati
applicati nel caso della nave possono essere applicati anche in questo. E’
stato trovato che il coefficiente di resistenza lineare equivalente dipende
dall'ampiezza del movimento relativo fra l’elemento considerato ed il liquido
e, poiché il movimento dell’elemento dipende dal movimento risultante della
piattaforma, devono essere impiegati procedure iterative per il calcolo della
soluzione. La
forza fluida per unità di lunghezza data dalla equazione (7) può essere
integrata sulla lunghezza di ogni elemento ed essere sostituita dalle forze e
dai momenti staticamente equivalenti alle estremità di ogni elemento in
dimensioni consistenti con il metodo d’analisi delle strutture spaziali. La
risposta strutturale è quindi ottenuta con l'uso di un codice di calcolo
destinato ad un usuale calcolo ad elementi finiti oppure ad un calcolo
strutturale spaziale. I regolamenti per il disegno strutturale delle
piattaforme in mare aperto sono redatti dalle Società di classificazione
nazionale. Valutazione
probabilistica dei carichi indotti dalle onde in stati di mare confuso L'analisi
statistica, suffragata dagli esperimenti su modello, da misure al vero e da
strumenti di calcolo idonei, è ora riconosciuta come facente parte del
processo, accettato ed importante, di valutazione del momenti flettente e
degli altri carichi che agiscono su una nave in moto ondoso. Roop
ha tentato per primo un metodo statistico limitato al problema dei carichi e
degli sforzi di flessione longitudinale su una cisterna navale. Le analisi
statistiche da allora sono state applicate ai dati in grande scala degli
sforzi della nave, Bimingham. L’ultimo è stato uno studio probabilistico in
cui sono state calcolate le ampiezze del momento flettente in onde regolari
differenti per sette navi dalle cui prove erano state registrate le onde.
Sono stati calcolati i momenti flettenti a breve termine per gli spettri
dell'onda che rappresentavano differenti stati di mare e successivamente sono
stati previsti i carichi operativi per un funzionamento di 14 anni
nell'Atlantico del Nord in base ad un certo numero di ipotesi per quanto
riguarda gli effetti degli angoli d’incontro della nave, della velocità,
degli spettri dell'onda, ecc. Nel
frattempo, in molti paesi è stato orientato uno sforzo continuo verso i
metodi probabilistici di valutazione dei carichi d'onda sulle navi
mercantili, patrocinato ed effettuato principalmente dalle società di
classificazione e dal S.S.C.. Questo lavoro è ricapitolato regolarmente negli
atti del Congresso Internazionale delle Strutture Navali (ISSC). Come
spiegato nel paragrafo 4, le risposte strutturali a stati di mare confuso –
così come i movimenti - sono previste solitamente dalla combinazione lineare
delle risposte ad una serie di onde regolari elementari. Nell'applicazione
del combinazione, è necessario ipotizzare che i carichi siano correlati
linearmente con le ampiezze delle onde anche quando estrapolati ai valori
degli stati di mare più severi. Ci sono state parecchie indagini sperimentali
finalizzate alla verifica di questo presupposto esaminando i momenti
flettenti in mezzeria rilevati sperimentalmente in onde con altezza
progressivamente crescente. Il presupposto delle linearità è stato trovato
solitamente cautelativo, cioè, la percentuale di aumento misurato del momento
flettente in mezzeria è minore dell’aumento dell'ampiezza delle onde nella
gamma delle onde più ripide. Tuttavia, è importante ricordare i presupposti e
le limitazioni dell’analisi lineare quando si utilizzano i carichi che sono
calcolati per mezzo di codici di calcolo lineare dei movimenti della nave. Si
guardi a tale proposito la discussione sulla validità della teoria lineare. Nel
quadro della teoria lineare del movimento della nave, tutti i componenti di
carico sullo scafo indotti dai movimenti dovuti al moto ondoso, compresa la
pressione in un punto della superficie dello scafo, il carico idrodinamico
per unità di lunghezza, il carico inerziale per unità di lunghezza, la forza
di taglio ed il momento flettente, sono collegati linearmente con l'ampiezza
dell'onda. Quando il principio della combinazione lineare è usato nella
predizione della risposta in un mare confuso, i metodi discussi nell’apposito
paragrafo possono essere applicati nella valutazione delle probabilità di
risposta a breve termine. Se questa valutazione si riferisce ad un componente
del carico - per esempio il momento flettente in mezzeria – c’è solitamente
un valore medio diverso da zero di momento in acqua tranquilla al quale il
momento indotto dalle onde deve essere sovrapposto. Le probabilità del carico
possono allora essere calcolate prendendo in considerazione la combinazione
del momento indotto dalle onde e di quello in acqua tranquilla. Le quantità
statistiche che sono solitamente degne di nota nelle indagini di resistenza
delle piattaforma o delle navi sono divise in tre categorie: -
valori medi ed estremi a breve termine -
valori medi ed estremi a lungo termine -
valori ciclici cumulativi Valori medi ed estremi a
breve termine Nella
prima categoria “breve termine” si riferisce ad un periodo approssimato da
una a quattro ore durante il quale è stato trovato che lo stato di mare
rimane pressoché uniforme (cioè, statisticamente stazionario) in circostanze
climatiche normali. Una discussione sui principi generali delle probabilità a
breve termine e sulla loro applicazione al problema dei carichi sullo scafo è
stata trattata nel successivo paragrafo. Valori medi ed estremi a
lungo termine La
seconda categoria si riferisce ad un periodo di tempo più lungo, che può
essere misurato in giorni o anni, durante il quale gli stati di mare possono
variare ampiamente da uno stato di calma ad uno di tempesta severa, ma la
velocità alla quale tali stati si modificano è sufficientemente bassa che il
presupposto di uniformità è di buona approssimazione durante il periodo di
poche ore. Quindi, la risposta a lungo termine può essere pensata come una
somma delle risposte a breve termine di differenti stati di mare, avente
ciascuno caratteristiche uniforme o statisticamente stazionarie. Questa
accumulazione di esperienze a breve termine si estenderebbe, nel caso di navi
e di strutture oceaniche, per un periodo di tempo uguale alla durata di
funzionamento utile da venti a trenta anni. Questo metodo è discusso nel
paragrafo Valori estremi a lungo
termine. Valori ciclici cumulativi La
terza categoria nella suddetta lista si riferisce al fenomeno di carico ciclico
di lungo termine che può causare un danno cumulativo a fatica per la
struttura. Qui i numerosi cicli da livello basso a moderato del momento
flettente e delle tensioni possono contribuire ad un danno paragonabile a
quello causato da pochi cicli di sforzo estremo. Per questo deve essere
considerata la gamma completa dei carichi indotti dalle onde, compresi i
valori moderati più numerosi ed i termini elevati meno frequenti. Sarà
mostrato nel seguito che le informazioni più importanti sul carico ciclico
possono essere ricavate dalla seconda categoria di dati a lungo termine, una
volta espresse come probabilità di superamento. Un’ulteriore discussione
sulla fatica è contenuta nel paragrafo CARICHI
DINAMICI. Valutazioni
dei carichi a breve termine in stati di mare confuso Per
gli scopi del progetto strutturale è necessario avere informazioni riguardo
ai valori dei carichi molto elevati o estremi piuttosto che una massa di
valori medi. In generale ci sono due approcci al problema: Probabilità
di supero e teoria
del valore estremo. La
valutazione della probabilità di supero è più semplice, dato che se
conosciamo la funzione di densità dei carichi, questa curva può essere
integrata per dare la probabilità di supero ai differenti livelli di carico,
quindi del valore che penseremmo sia oltrepassato una volta in un certo
numero di cicli. Ma se noi conosciamo la funzione di densità, possiamo anche
applicare i principi del calcolo convenzionale del valore estremo per
ottenere il più alto valore previsto in un certo numero di cicli. Di solito
il valore da oltrepassare una volta ed il valore più alto sono quasi uguali
ed il primo è adatto agli scopi progettuali. La
statistica a breve termine dei massimi o dei picchi di qualsiasi risposta,
compreso il momento flettente o gli sforzi, possono essere determinati a
partire dai momenti dello spettro di risposta. Per scopi pratici è
solitamente possibile ipotizzare un processo a banda stretta, nel qual caso
le statistiche sono definite da una funzione di densità di Rayleigh (cioè,
ε=0). La corrispondente funzione di distribuzione (cumulativa) di
Rayleigh definisce la probabilità di non supero dei differenti livelli di
carico o di sforzo. Ma qui Q è considerata come la probabilità di supero dei
vari livelli. Quindi, la funzione di distribuzione è (1 - Q). Poiché la
funzione di densità di Rayleigh è:
la
probabilità di supero è:
Quindi,
la probabilità di supero può essere calcolata facilmente come funzione del
parametro, mo. Il numero di cicli, n, al quale un valore si pensa
sia uguale o ecceda x1 (il periodo di ritorno) è, n = 1/Q = exp [
x12 / 2*mo ]. La quantità mo è la
varianza statistica del processo stocastico, uguale al momento zero o area
dello spettro del processo ed il valore √mo è il valore di
rms. A
volte i progettisti preferiscono lavorare con il più alto valore previsto del
carico, che è calcolato sulla base della teoria degli estremi. Oltre al breve
termine i valori estremi per il massimo di un processo stocastico a banda
stretta sono forniti da un'espressione della forma:
Il
valore estremo in questione, Yn, è definito come il valore
previsto della più alta singola escursione o massimo in un campione di n
escursioni. Cn è una costante dipendente da n, approssimativamente
2√ln(n), per grandi valori di n. Come
conseguenza della casualità del mare e delle risposte della nave, sia il
valore previsto di supero che il valore massimo previsto sono soggetti a
variazioni. Così se molte registrazioni fossero prese su molte navi nello
stesso stato di mare, il valore più alto di alcune delle registrazioni
sarebbe più grande del valore previsto calcolato dall’equazione (10) e di
altre sarebbe più basso. I valori di picco per determinati n saranno quindi
caratterizzati da una loro propria distribuzione di probabilità che avranno
una dispersione rispetto ad un valore medio. Riguardo all’esperienza di una
singola nave che subisce un totale di n oscillazioni di momento flettente, il
valore dato dalla (10) deve essere interpretato come la valutazione del
valore medio o del valore previsto del più alto picco. In alcune analisi è
usato il valore modale o più probabile anziché la media e questo è dato da
un'espressione simile alla (10) ma con i valori modificati del coefficiente,
Cn. Per n superiore a 1000, che è tipico di tre o quattro ore di
moto ondoso, i valori modali e medi risultano quasi identici. Per
ottenere una stima più utile del valore estremo che rifletta la casualità dei
picchi, Ochi ha applicato alla probabilità di supero il parametro di rischio
α. La stima del valore del picco estremo in una sequenza di n escursioni
è ancora dato da un'espressione della forma di (10), ma la costante Cn
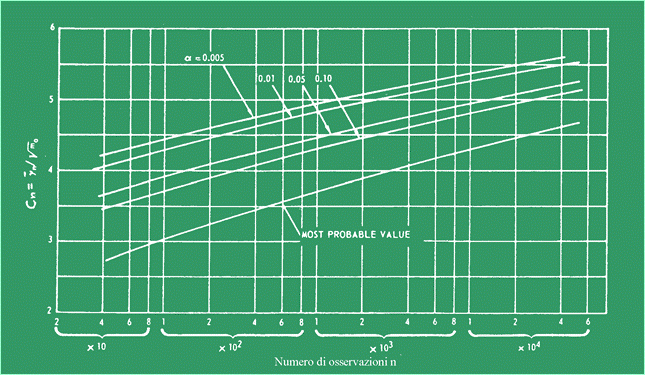
è ora una funzione della α così come di n. La Figura 12 presenta valori
di Cn modificato per il processo stocastico a banda stretta come
funzione del parametro di rischio α.
Figura 12 Così
il valore stimato del più alto momento flettente per un parametro di rischio
di 0.01, è dato dall’equazione (10) con Cn preso dalla Figura 12 e
questo valore si applicherà a tutte le navi in una flotta ipotetica di tante
navi simili. Se noi ora esaminassimo le registrazioni del momento flettente
per tutte le navi nello stesso stato di mare ed estraessimo da ogni
registrazione il singolo picco più alto, troveremmo che con α=0.01 il
valore stimato dalla presente procedura è oltrepassato dai valori misurati al
vero approssimativamente dall’un per cento delle navi. Si noti che se
avessimo stimato il valore più probabile per il picco del momento flettente,
avremmo potuto trovare il valore stimato superato dal valore reale approssimativamente
nel 63 % delle navi. Abbiamo
visto nella Figura 12 che Cn aumenta pochissimo quando α
assume valori minori di 0.01. Per questo motivo, un valore di α=0.01 è a
volte considerato adatto agli scopi progettuali, a condizione che si stia
considerando una singola situazione a breve termine ove siano note la
condizione del mare (spettro) e la relativa durata. La
suddetta teoria, applicabile alle situazioni a beve termine, è d’utilità
diretta limitata per il progetto della nave, poiché per gli scopi principali
del progetto dobbiamo tenere conto delle varie e differenti condizioni del
mare che devono essere incontrate dalla nave durante il corso della vita
operativa. Tuttavia, se fossimo capaci di definire lo spettro dello stato di
mare più severo, che una struttura quale una piattaforma fissa potrebbe
essere in grado di sopportare, oltre alla relativa durata (persistenza), noi
potremmo predire il più alto carico previsto mediante le tecniche del breve
termine. L'idea
di progettare con carichi che corrispondono ad un'estrapolazione delle onde
estreme alle più alte previste in un periodo di 50 o 100 anni è stata usata
molto nell'ingegneria civile e recentemente in alcuni rami dell’ingegneria
navale. La pratica in vigore nel progetto delle piattaforme “off-shore” per
il Mare del Nord è di progettare per "la tempesta dei 100 anni". Le
altezze d'onda ed i periodi corrispondenti sono stati derivati dalle analisi
dei dati delle onde utilizzando la teoria del valore estremo. Dovrebbe essere
notato in questo contesto che il valore dell'onda estrema è l’"estremo
più probabile" ed ancora che c’è una probabilità significativa di
superare questo livello nel primo, o successivo, dei campioni di lunghezza
uguale al periodo di ritorno. Di conseguenza, un certo margine di progetto
deve essere definito, nei fattori di sicurezza usati successivamente, o nella
definizione di un adeguato periodo di ritorno di progetto. Per esempio, se è
gradito fissare un valore estremo per il progetto in modo che vi sia un 80
per cento di probabilità che il valore non sia oltrepassato in un'esposizione
di 20 anni, il periodo di ritorno di progetto può essere definito come [
20/(1-0.8) ] = 100 anni. Si
noti inoltre che il suddetto metodo suppone che il più severo stato di mare
produrrà il più alto carico. Questo potrà essere vero per una piattaforma
fissa, ma non lo potrà essere necessariamente per navi ed altre strutture
galleggianti. Il carico estremo dipende dalle caratteristiche di risposta
della nave o di altre strutture, così come dal tempo previsto di esposizione
(probabilità e durata degli stati di mare severi). Valori
estremi a lungo termine Quando
dobbiamo occuparci della previsione del carico più severo che può essere affrontato
da una nave o da una struttura durante l’intero corso della sua vita utile,
non possiamo più ammettere che le condizioni del mare o gli stati di
funzionamento della nave possano rimanere costanti. Possono essere incontrati
stati di mare di severità variabile dalla calma piatta alla tempesta più
violenta e l’accadimento e la durata delle condizioni del mare nei vari gradi
di severità dipenderanno dal profilo operativo geografico e stagionale della
nave o della piattaforma. Gli stati di carico, di velocità e di rotta
varieranno da un periodo di tempo ad un altro e l'influenza di tutte queste
variabili deve essere inclusa nel calcolo del carico estremo a lungo termine.
Come nel caso del breve termine, non è generalmente possibile ottenere un
singolo preciso valore per il carico più alto. Invece, la risposta deve
essere espressa sotto forma di probabilità a lungo termine. Ci
sono i due approcci fondamentali - come nel caso del breve termine - di
probabilità di supero e teoria del valore estremo. Nonostante l’ultimo
approccio non sia adatto a fornire i dati ciclici di carico per i problemi di
fatica, questi ha fornito un metodo utile di estrapolazione dei dati estremi
osservati del carico agente e dell'onda incontrata in navigazione al caso
dell’analisi a lungo termine. Il metodo più comune coinvolge la valutazione
delle probabilità di supero, o quella che è stata denominata distribuzione a
lungo termine, che sono distribuzioni iniziali sintetizzate dei massimi di
risposta, o probabilità di supero per ciclo di carico. Ci sono attualmente
una dozzina di metodi in uso per ottenere tali distribuzioni a lungo termine.
Oltre che l’ipotesi di linearità della risposta, un presupposto fondamentale
fatto in tutti i metodi è che a breve termine i massimi della risposta
abbiano una struttura di probabilità definita tramite la distribuzione di
Rayleigh (ε=0); cioè che a breve termine la risposta è un processo a
banda stretta gaussiano stazionario a media-zero con i massimi definiti dal
singolo parametro, mo = σ2. Le probabilità a breve
termine sono condizionali, cioè, presuppongono valori differenti per ogni
valore di mo. Nello specifico, la densità può essere scritta:
dove
mo è il momento spettrale zero che rappresenta la risposta media
quadratica di ogni esposizione a breve termine. Questo singolo parametro, mo,
definente una distribuzione di Rayleigh è considerato come una variabile
casuale dipendendo dalla condizione del mare, dalla velocità, dal carico e
dall’angolo di incontro della nave durante ogni intervallo a breve termine. A
causa dei presupposti dichiarati innanzi il seguente sviluppo della teoria si
pensa possa essere cautelativo. Per ottenere una distribuzione a lungo
termine è necessario considerare molti intervalli differenti a breve termine,
in ciascuno dei quali la risposta è definita da mo. Questa è la
ragione per cui la geometria e le caratteristiche della nave sono inserite
nell'analisi. I fattori che interessano il valore di mo includono
la velocità V, l’angolo di incontro μ, lo stato di caricazione, una
misura di altezza d'onda, H, qualche misura del periodo dell'onda, quale Tm,
il periodo modale, ed a volte un'altra misura della forma o della figura
spettrale dell'onda. Per
sviluppare una distribuzione a lungo termine in pratica, sono necessarie
alcune semplificazioni. La velocità, V, può essere eliminata riconoscendo che
non è una variabile indipendente e specificando che per ogni intervallo di
tempo la velocità è quella che è adatta per la condizione del mare
prevalente, per la caricazione e per l’angolo d’incontro nave-onda da cui
dipende. (Si noti che il momento flettente in ogni caso non è influenzato
notevolmente dalla velocità della nave) La variabile dell'angolo di incontro,
μ, non può essere eliminata, ma è consueto supporre che vi è una
probabilità uguale per tutti gli angoli di incontro, quindi è statisticamente
indipendente dalle altre variabili. Ciò non può essere vero su qualsiasi
viaggio, ma tende ad essere tale considerando molti viaggi ripetitivi. Per
concludere, il carico può essere trattato supponendo che il numero di
condizioni sia limitato (viaggi con
carico alla marca e ritorno in zavorra), ciascuno con un momento
flettente medio (in acqua tranquilla) differente e che possono allora essere
effettuati per ciascuna di queste condizioni calcoli completamente
indipendenti. Supponendo che due parametri, H e T, siano sufficienti per
descrivere lo stato di mare, si assumeranno i parametri, μ, H e T. Se
i suddetti fattori saranno assunti per essere variabili casuali, quindi anche
il momento spettrale, mo, lo è e la relativa densità di
probabilità è condizionale. Riconoscendo i rapporti condizionali fra la
risposta, x, ed mo ed il rapporto condizionale fra mo e
tutti gli altri fattori enumerati innanzi, una densità di probabilità a lungo
termine può essere assunta nella seguente forma:
dove
il primo fattore è la densità condizionale a breve termine della x, equazione
(11) ed il secondo è la densità condizionale di mo, dati i fattori
operativi ed ambientali. Per concludere, l'ultimo fattore è la densità congiunta
di probabilità dei parametri che influenzano mo. Per
ottenere la densità di probabilità a lungo termine della risposta, x,
l'equazione (12) deve essere integrata riguardo ad mo, μ, H e
T. Tuttavia, la probabilità a lungo termine di interesse è quella dei picchi
di risposta o dei massimi della x che eccedono un certo livello, ad esempio x1.
Questa è ottenuta integrando la densità di probabilità a lungo termine della
x riguardo alla x nell'intervallo da x1 all'infinito. Nell’ipotesi
di Rayleigh, e dell’equazione (11), quest’ultima integrazione può essere
fatta formalmente, di modo che alla fine la probabilità a lungo termine che
una risposta ecceda x1 può essere scritta:
Lo
sviluppo di una procedura d’ingegneria utilizzabile richiede quindi la
sintesi delle probabilità congiunte e condizionali e la loro integrazione, ed
è qui che comincia la divergenza nei vari metodi esistenti. Non conosciamo le
esatte densità di probabilità di nessuno dei fattori coinvolti, molto meno la
forma della loro densità congiunta. I tecnici dei vari metodi hanno dovuto
interpretare i dati storici degli stati di mare, adottare mezzi per
utilizzarli nelle integrazioni richieste, adottare ancora mezzi per trattare
la velocità, l’angolo di incontro ed i fattori di caricazione ed infine hanno
avuto la scelta dell'ordine di integrazione. Il risultato è che i vari metodi
sembrano differire più di quanto lo fossero fondamentalmente. Qualunque sia il
metodo il risultato finale è una distribuzione iniziale definita
numericamente dei massimi nella grande messe di distribuzioni a breve termine
di Rayleigh, che in effetti sono sovrapposte nella sintesi. Alcuni scelgono
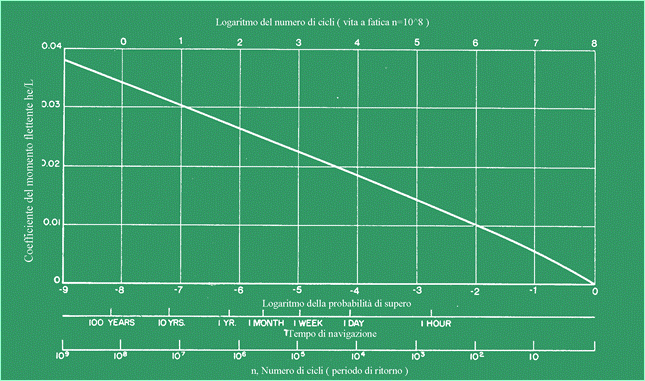
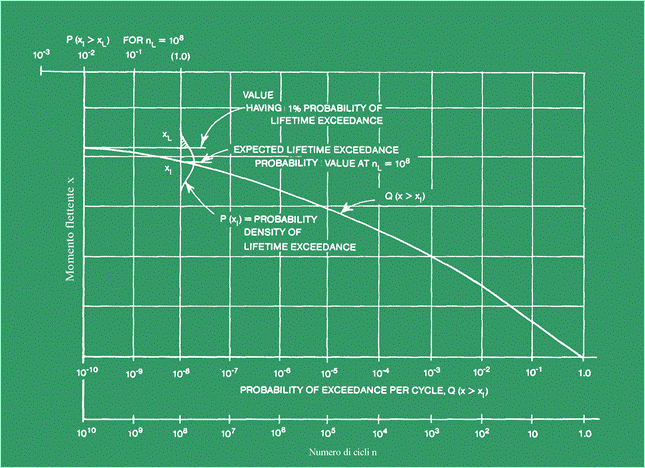
tracciare i risultati su una carta probabilistica. La Figura 13 da Band, è
una forma piuttosto comune della presentazione.
Figura 13 L'ordinata
è il livello x1, nell'equazione qui sopra. L'ascissa è una scala
logaritmica di Q (x> x1), o il relativo reciproco, n,
conosciuto come il periodo di ritorno (entrambi sono indicati nella figura).
È importante notare che i risultati della formulazione della probabilità solo
che il picco di un'escursione della risposta, scelto a caso, sia più grande
di un certo livello (nell'esempio la probabilità è circa 10-8 che
il coefficiente di momento flettente ecceda circa 0.035). Approssimativamente,
la formulazione coinvolge la probabilità per ciclo di risposta. Questa è la
ragione per cui i calcoli sono effettuati per tali basse probabilità. La
scala ausiliaria nella figura indica approssimativamente, sulla base dei
periodi medi d’incontro per la nave, il tempo d’esposizione e come può essere
notato è necessario considerare probabilità minori di 10-7 per
rappresentare le vite della nave ed i suoi multipli. Per
illustrare le considerazioni assunte nei metodi di previsione a lungo termine
faremo una semplificazione particolare dell'equazione (13). Si supponga che
le gamme di tutte le variabili, μ, H e T siano sistematicamente divisi
in intervalli discreti di larghezza tale che il valore della variabile al
centro dell'intervallo è rappresentativo della variabile ovunque
nell'intervallo. Con questo presupposto l’equazione (13) può essere
approssimata come sommatoria:
dove
è implicito che sono stati considerati i valori centrali discreti delle
variabili. La funzione, p (μ, H, T) denota la probabilità che le
variabili, μ, H e T si trovino simultaneamente nei loro rispettivi
intervalli. In questa forma la probabilità condizionale del momento
spettrale, mo, rappresenta la variazione statistica di questo
parametro riguardo al valore che sarebbe stato valutato considerando ciascuno
dei valori centrali riparati e applicando i metodi noti. Ora
per gli scopi attuali possiamo fare un’ulteriore assunzione semplificativa.
Si supponga che gli intervalli in cui il campo delle variabili, μ, H, T
sono suddivisi siano sufficientemente piccoli che il momento spettrale che
può essere valutato considerando i valori centrali delle variabili fissate,
sia anche rappresentativo del momento che sarebbe stato ottenuto a condizione
che le variabili μ, H, T fossero state ovunque all'interno dei limiti
dei loro rispettivi intervalli. Tutto questo per dire che il momento
spettrale, mo, è una funzione deterministica dell'angolo
d’incontro della nave e dello stato di mare. Con questo presupposto la
probabilità condizionale nell'equazione (14) tende verso una funzione delta e
quando è effettuata integrazione rispetto a mo l'espressione si trasforma in:
dove
la notazione è stata migliorata per facilitare ulteriori sviluppi. In
particolare, le sommatorie sono eccedenti rispetto a tutti gli intervalli
discreti precedentemente definiti e gli argomenti della probabilità unita
simbolizzano i valori centrali definiti insieme con l'equazione (14). Ancora
più importante, il valore di mo nell'esponenziale è preso come
funzione deterministica dei valori centrali delle variabili operative ed
ambientali. In questa forma il problema della sintesi diventa quello di
costruire una rappresentazione discreta della probabilità congiunta. Per
illustrare come questa probabilità congiunta potrebbe essere costruita si può
argomentare come segue. Immaginiamo la vita della nave suddivisa in
tantissimi intervalli di breve termine, per esempio, 4 ore ciascuno, durante
i quali gli stati di caricazione, di velocità della nave, dell'angolo
d’incontro e dello stato di mare rimangano costanti. Ora, si supponga che i
valori di tutti i parametri, μ, H, T siano conosciuti per ciascuno di
questi intervalli di tempo. Ciò, in effetti richiede che siamo capaci di
predire il profilo operativo della nave nei termini della sua caricazione,
velocità ed angoli d’incontro oltre che delle condizioni atmosferiche che
incontrerà. Le previsioni della caricazione della nave, della velocità e del
tragitto sono effettuate normalmente dall’armatore o dal progettista della
nave come una parte del processo preliminare di progettazione. Le previsioni
del mare e delle condizioni atmosferiche che la nave incontrerà dipendono
dalla disponibilità di una base di dati degli stati di mare di forma ed
estensione opportuna. Nell'equazione
(15) lo stato di mare è rappresentato da due parametri, la misura
dell’altezza, H e del periodo T. In alcune formule spettrali, soltanto un
parametro, per esempio l’altezza significativa, H1/3 è usata per
caratterizzare lo stato di mare. In altri è impiegato il parametro ulteriore,
Tz, periodo zero-crossing, o Tm, periodo modale, al
fine di dare mezzi più flessibili per rappresentare una vasta gamma dei
spettri di aspetto o forma simile (cioè delle famiglie). Idealmente, dovrebbe
essere considerata anche la variazione nella figura degli spettri, poiché gli
spettri degli stati di mare oceanico misurati al vero mostrano una
considerevole varietà compresi i doppi picchi che derivano dalla
sovrapposizione di onde provenienti da due o più tempeste. Ma per semplicità
spesso si considera che due parametri bastino. La
frequenza di occorrenza a lungo termine di stati di mare di differente
severità ma dalla forma spettrale simile può allora essere espresso in
termini di funzione di densità di probabilità congiunta per H1/3 e
Tm. Questa densità di probabilità congiunta di H1/3 e Tm
può essere rappresentata, per una data zona dell'oceano, sotto forma di
tabella, come in Hogben ed in Lumb, o di un diagramma come indicato nella
Figura 14.
Figura 14 I
valori nelle tabelle, o nel diagramma, sono uguali alla probabilità (frazione
del tempo) che lo stato di mare sia caratterizzato dall’accadimento
simultaneo dei valori di H che fanno parte dell'intervallo da H1
ad H2 e di T che fanno parte da T1 a T2.
Questo presupporrebbe una singola forma per lo spettro (per esempio
Bretschneider o JONSWAP). Se la nave opera in zone geografiche differenti che
hanno stati di mare differenti, tali diagrammi sarebbero richiesti per ogni
zona operativa del mare. Una
distribuzione composta degli stati di mare può essere costruita se abbiamo
tali tabelle o schemi per tutte le zone operative della nave insieme alle
informazioni riguardo alla frazione di tempo che la nave trascorrerà in ogni
zona. Per illustrare questa sintesi, si consideri una cisterna che transita
tra l’Europa ed il Golfo Persico attraverso il Capo di Buona Speranza. I
tratti tropicali dell'itinerario sarebbero caratterizzati da una
preponderanza di mare calmo mentre i tratti del Capo sarebbero caratterizzati
in larga parte da stati di mare agitato. Sarebbe quindi necessaria una serie
di schemi simili alla Figura 14, o una tabulazione della frequenza di
accadimento degli accoppiamenti dei valori di H1/3 e Tm
per rappresentare questi estremi così come le variazioni degli stati del mare
tipici di altre parti dell'itinerario. Ora, poiché ogni diagramma “scatter”
è, infatti, una funzione bivariata di densità di probabilità che rappresenta
la frequenza relativa di accadimento degli stati di mare in tutti i gradi di
severità nella zona applicabile dell'oceano, l'integrale del diagramma su
tutti i valori di H1/3 e T deve essere uguale all'unità. La
struttura sarà, comunque, esposta in zone geografiche differenti per periodi
di tempo differenti durante ogni frazione del suo viaggio. Le ordinate del
diagramma “scatter” per ogni zona lungo l'itinerario devono, quindi, essere
moltiplicate per la frazione che esprime la proporzione di tempo che la nave
trascorrerà in quella zona. E’ costruito allora uno schema o una tabulazione
composta per l'intero viaggio aggiungendo le ordinate pesate di tutti gli
schemi che rappresentano i segmenti di viaggio. Per
ogni insieme di valori delle variabili, μ, H1/3 e Tm
ora possiamo determinare la risposta del carico della nave e calcolare un
valore del momento spettrale, mo, della caricazione. Questo
calcolo normalmente viene effettuato usando uno dei movimenti della nave e
dei programmi di caricazione standard. La sommatoria nell'equazione (15)
allora si approssima con:
La
forma semplice del prodotto dell'equazione (16) è basato sul presupposto che
tutte le variabili casuali restanti siano statisticamente indipendenti. In
effetti stiamo facendo un sovrapposizione di molte distribuzioni di Rayleigh,
pesate dalla frequenza prevista di accadimento di tutte le combinazioni delle
tre variabili. Per usare i risultati forniti dall’equazione (16) nella
selezione del valore del carico di progetto, dobbiamo scegliere un carico che
ha una probabilità di accadimento accettabilmente bassa e, concettualmente,
possiamo continuare nel ragionamento progettuale come segue. Il periodo medio
dell'onda d’incontro in mare è di circa dieci secondi. Nel corso della vita
di venti - venticinque anni, la nave incontrerà approssimativamente 108 onde,
ed il valore esatto dipenderà dal profilo operativo e dalla parte del tempo
trascorsa in mare. È ragionevole progettare la struttura in modo che la nave
sia capace di sopravvivere al più alto singolo picco di escursione del
momento flettente o di un altro carico prevedibile nel corso della vita; così
il carico che ha una probabilità di supero di una volta in 108
cicli sembrerebbe essere un valore ragionevole da raggiungere. L'equazione
(16) esprime la probabilità che alcun picco di oscillazione ecceda il valore
x1. Tuttavia,
dovrebbe essere notato che il carico che corrisponde a questa probabilità è
soggetto a variazione, come nel caso del breve termine. Quindi, durante il
corso della vita della nave, ci può essere un valore di picco che supererà il
valore che corrisponde alla probabilità 10-8, potrà non essere
alcuno o potranno essere vari. Se la nave navigherà per altri venti anni
nello stesso servizio, o se consideriamo una seconda nave identica, questo
valore 10-8 potrà essere oltrepassato una o più volte ancora. Se
sarà oltrepassato ancora, il secondo supero potrà essere con un margine molto
più grande di quello sperimentato la prima volta o potrà essere con un
margine minore. Il problema è simile a quello dell'esperienza a breve termine
in cui il parametro di rischio è stato introdotto per misurare le valutazioni
probabilistiche degli eventi estremi. Questo comportamento casuale del più
alto carico di picco previsto può essere preso in considerazione usando una
procedura suggerita da Karst. Questi formula un problema che può essere
riesposto così: per determinare un momento flettente (o sforzo) xL
tale che la probabilità che una nave lo ecceda nel corso della vita abbia uno
specifico valore P( x> x1 ), in cui x1 è il momento
flettente previsto che corrisponde ad una vita di nL massimi (o
cicli) Q( x > x1 ) = 1/nL. La probabilità specifica
P(x1>xL ) è un fattore di rischio o livello di
confidenza analogo all”α” di Ochi, precedentemente discusso. In base ad
un modello di Poisson, il risultato approssimato è che il momento flettente
di progetto xL può essere letto da
La
procedura è illustrata nella Figura 15, ove è mostrato un grafico della
funzione Q(x> x1)=1/n tracciata nel modo usuale. Ad un livello
di probabilità di 10-8, l'ordinata della curva è il valore
previsto del carico (momento flettente in mezzeria) che ha questa probabilità
di supero in un qualsiasi ciclo.
Figura 15 Il
grafico piccolo tracciato lungo l'asse verticale a questo livello di
probabilità è, schematicamente, la funzione di densità di probabilità dei
valori di picco a 1/108 sulla vita della nave. Questa funzione di
densità esprime il comportamento casuale dei picchi più alti che accadono in
molte registrazioni che contengono ognuna nL picchi. Il contorno
della porzione tratteggiata di questa funzione di densità di probabilità
corrisponde al valore dell’un per cento, cioè, la zona tratteggiata è uguale
all’un per cento dell’area totale sotto la curva. Quindi, P(x1
> xL) = 0.01= 10-2. Se estrapoliamo questo un per
cento su una linea orizzontale verso sinistra, questo interseca la curva
Q(x>x1) molto vicino alla probabilità 10-10, che è
il valore dato dalla equazione (17). Questo costituisce una via conveniente
per ottenere Q(x> x1)
per una P(x1 > xL) = 0.01 estrapolando la
curva a lungo termine su valori più bassi di probabilità. Il significato di
questo risultato è che si definisce un carico di progetto che potrebbe essere
atteso di essere superato una volta su una qualsiasi nave in una flotta di
100 navi simili che prestano lo stesso servizio. Per
esempio, se noi imponiamo P(x1 > xL) uguale a 0.01
ed nL uguale a 108, troviamo che, con buona
approssimazione, il carico di progetto xL, può essere letto a
Q(x>xL) = 10-2 / 108 = 10-10.
Con questo si vede che il livello di confidenza un per cento è ottenuto
usando il carico di progetto xL corrispondente alla probabilità di
supero Q(x>xL) che abbia un valore uguale al prodotto del
fattore di rischio ( o livello di confidenza) ed una probabilità di supero
attesa nella vita della nave di nL cicli. In alternativa, la
probabilità di sopravvivenza (fattore di rischio) è:
Si
note che le equazioni (17) e (18) si suddividono, comunque, quando xL
= x1 o Q(x>xL) = l/nL. Nel nostro caso
P(x1 > xL) è 0.667 anziché P(x1 > xL)
= nL * 1/nL = 1.0, come dato dall’equazione (18). Si
veda la Figura 15. L’equazione
(18) è utile nel calcolo della probabilità di collasso, dato che il fattore
di rischio P(x1 >xL) può anche essere considerato
come la probabilità che qualsiasi nave in una flotta di molte navi simili
supererà il valore di carico xL di progetto durante la sua vita.
Quindi, a volte ci si riferisce a questo come probabilità di sopravvivenza
per distinguerlo dalla probabilità per ciclo, Q(x>xL), o 1/n.
Si noti inoltre che una curva di P(x1 > xL) può essere
ottenuta per ogni valore di nL aggiungendo una nuova scala al
diagramma di Q(x>xL). Per esempio, una scala di P(x1>xL)
è stata aggiunta alla parte superiore della Figura 14 per nL = 108. L'analisi
precedente restituisce una valutazione del valore della probabilità di supero
prevista durante il lungo periodo di esposizione in cui si incontrano la
gamma completa di variazione delle velocità, degli angoli di incontro di
altre variabili. L'equazione (16) è basata sulla distribuzione di Rayleigh
per i valori di picco del processo casuale e, come precisato da Ochi, non
contiene esplicitamente il periodo d’esposizione. Invece, si dovrebbe pensare
a come applicarlo ad un largo numero di escursioni di picco valutato
approssimativamente durante la vita della nave. Per calcolare esattamente il
numero di picchi di oscillazione nel periodo di tempo, operiamo come segue.
Durante uno degli intervalli a breve termine in cui le variabili, μ, H1/3
e Tm rimangono costanti, il numero medio di zero-crossing nell’unità di tempo
è dato da:
Qui,
m2, è il secondo momento dello spettro della risposta. È coerente
con il presupposto di Rayleigh che ad ogni passaggio sullo zero corrisponde
un picco del processo casuale, di modo che l'equazione (19) darà inoltre il
numero di picchi nell’unità di tempo, nz. Ora, se T è uguale al
periodo a lungo termine in ore, il tempo totale durante il quale un gruppo
specifico di variabili, μi, Hj e Tk,
possa prevalere è dato da:
ed
il numero totale di oscillazioni durante il tempo T da:
Per
comprendere questo numero nel calcolo della probabilità, Q, ogni termine
nell'equazione (16) deve essere ora moltiplicato per una funzione che ne
determini il peso che è costituita dal rapporto del numero di picchi di
oscillazione corrispondente a ciascuno
degli intervalli della sommatoria., al numero totale di picchi dati
dall’equazione (21), nz* = nz(μ, H, T) / Σ nz p(μ) p(H)
p(T) anziché 1.0, come presupposto nell'equazione (16). Quindi, il risultato
finale, modificato per esprimere la probabilità in termini di tempo, è
Lewis
e Zubaly hanno valutato un esempio che indica che i risultati ottenuti dalla
(16) e dalla (22) sono quasi gli stessi per la portacontenitori utilizzata
come esempio. Questo è spiegato notando che i valori più alti di momento
flettente generalmente si presentano in mari di prua che corrispondono al
numero più grande di picchi, od alle più alte frequenze medie di
oscillazione. I carichi in mari di poppa sono generalmente molto più bassi e
danno pochissimo contributo alle probabilità complessive. La procedura precedente
conduce ad una valutazione dei valori di supero a lungo termine che prende in
considerazione tutti i differenti stati di mare che la nave può incontrare
durante la sua vita. La sommatoria pesata include i contributi del mare poco
mosso che accadono frequentemente ma individualmente hanno basse probabilità
di causare eventi estremi e degli stati di mare in tempesta, ciascuno dei
quali ha un'alta probabilità di causare un evento estremo ma che occorrono
relativamente poco di frequente. Come conseguenza della vasta gamma delle
circostanze da includere in un calcolo di questa natura, si vede che le
risorse di calcolo richieste possono essere considerevoli. Per
il problema del calcolo dei carichi ciclici per il calcolo a fatica, è
importante notare che la distribuzione a lungo termine discussa qui può
fornire le informazioni di base. La Figura 13 mostra una tal distribuzione,
con una scala di probabilità ed il numero di cicli nella parte inferiore. Se
la vita della nave per gli studi di fatica si ipotizza che corrisponda a 108
cicli, è stata riportata una nuova scala invertita, come indicato sulla parte
superiore, ove è riportato il numero di cicli previsti per raggiungere
qualsiasi specifico livello di momento flettente. Estrapolazione
dei valori estremi osservati Un
metodo alternativo al problema dei carichi di progetto considera soltanto i
più grandi massimi (estremi) nei campioni a breve termine anziché tutti i
massimi. Le applicazioni della teoria dei valori estremi sono presentate in
situazioni in cui la distribuzione iniziale è conosciuta nella forma chiusa,
come nel caso di un processo gaussiano stazionario a media nulla come una
registrazione di moto ondoso o una registrazione della risposta a breve
termine della nave in navigazione. La teoria può anche essere applicata ed
estesa al caso dell'estrapolazione dei dati storici a lungo termine sotto
forma di registrazione sia delle onde che delle risposte della nave. Se
sono disponibili i dati storici sugli estremi (cioè, i valori più alti) in
molti campioni di una popolazione, può essere utilizzato il metodo classico
di Gumbel per prevedere gli estremi che potrebbero probabilmente accadere in
futuro. Poiché la funzione di densità degli estremi tende ad essere più
concentrata della densità iniziale, possono essere derivate le forme
asintotiche della densità degli estremi che dipendono essenzialmente dalle
proprietà generali della densità iniziale. La Figura 16 da Yuille è inclusa
per illustrare il metodo. In questo caso particolare i dati erano le letture
quotidiane di un estensimetro meccanico installato su una nave da guerra.
Figura 16 Ogni
lettura è la massima oscillazione delle sollecitazioni sperimentate in un
giorno in mare e può essere interpretata così come l'estremo nel campione di
un giorno. Per analizzare un insieme N di tali osservazioni sono stati
organizzati per grandezza crescente e sono numerati con m = 1,2, … N,
convertendo così le osservazioni in sequenze statistiche. Sono state
calcolate le frazioni m/(N+1) per m = l, N e queste rappresentano una
valutazione della distribuzione di probabilità che corrisponde ad ogni livello
dell'osservazione. Il punto seguente è stato di presupporre una distribuzione
analitica ed adattarne i dati. La distribuzione assunta nell’esempio, Figura
16, era la prima distribuzione asintotica degli estremi. Il metodo usuale per
adattare i dati è di usare una carta probabilistica adatta alla distribuzione
presupposta. Le
frazioni sono tracciate su una tal carta nella Figura 16, dove la gamma delle
sollecitazioni è l'ordinata e la frequenza distorta o scala di probabilità è
l'ascissa. La scala di probabilità in tutte le carte probabilistiche è
distorta in modo tale che la distribuzione teorica risulti tracciata come una
linea retta. In
questo modo adattare i dati alla distribuzione assunta significa adattare la
migliore linea retta come indicato nell'esempio. Le linee tratteggiate nella
figura sono limiti di confidenza. Nell'esempio sono state calcolate in modo
tale che nella dispersione dei dati nei confronti della linea retta dovuto
agli errori casuali, può essere atteso, nell’intervallo tracciato dalle linee
tratteggiate, il 68 per cento dei dati. Queste linee forniscono un criterio
di verifica statistico per l'adeguatezza della misura dell'osservazione alla
distribuzione teorica presupposta. L’estrapolazione dei dati in modo da
prevedere gli estremi che hanno probabilità di accadere in eventi futuri è
stata fatta semplicemente estendendo la linea retta fino a livelli elevati di
probabilità. Dovrebbe essere notato riguardo ai dettagli dell’adattamento
nella Figura 16 che i dati sembrano deviare sistematicamente dalla linea
retta. Questo aumenta i punti che nessuna delle varie distribuzioni
analitiche che possono essere presupposte possa garantire il migliore
adattamento riguardo ad un dato insieme di dati. L'arte del metodo è di
trovare l'approssimazione analitica migliore. La distribuzione di Weibull è
stata utile a questo fine. Un
metodo ibrido interessante per il problema dei carichi di progetto è stato
discusso dettagliatamente da Ochi. Invece di integrare sopra tutti gli stati
di mare immaginabili sono derivate dai dati storici le circostanze più gravi
che hanno probabilità di accadere oltre alla loro persistenza (durata) e
tramite la teoria estrema a breve termine, con il fattore di rischio adatto,
è stata applicata soltanto alle risposte a questi mari in tempesta. Alcuni
confronti fatti con i risultati ottenuti con il metodo della somma pesata a
lungo termine mostrano un buono accordo. Il successo del metodo dipende
dall’abilità dell'utente nel considerare un numero sufficiente di mari
severi, tenendo conto delle loro probabilità e persistenza, per stabilire
chiaramente la risposta “più estrema”. Per la maggior parte dei problemi di
progetto della nave è suggerito il metodo a lungo termine descritto
precedentemente, poiché fornisce informazioni più complete, come i dati
ciclici di carico per fatica. Carichi
Dinamici Si
distinguono i seguenti carichi dinamici: -
springing ( Sobbalzare) -
carichi di slamming (Impatto) -
carichi inerziali sui componenti Springing Un
effetto importante delle onde del mare su alcune navi è l'eccitazione della
vibrazione casuale dello scafo che può continuare per lunghi periodi di
tempo. Questo fenomeno, conosciuto come springing, è stato notato
specialmente nelle porta rinfuse dei Grandi Laghi, ma è stato segnalato anche
sulle grandi navi d'alto mare con alti coefficienti di finezza. La
spiegazione è che le navi lunghe con bassa immersione ed altezza di
costruzione sono comparativamente flessibili nella flessione longitudinale e
conseguentemente hanno periodi naturali insolitamente lunghi della vibrazione
verticale dello scafo (periodi a due nodi di 2 sec o più). Gli studi
sperimentali e teorici hanno confermato che quando una tale nave sta
transitando nelle onde comparativamente corte che danno risonanza con il
periodo naturale di vibrazione, è prodotta una vibrazione significativa. Una
corrispondente fluttuazione nelle tensioni in mezzeria è quindi sovrapposta
alla sollecitazione di flessione dell'onda quasi statica. E’
stata applicata la già sviluppata “strip theory” allo springing nelle onde
corte. Anche se i movimenti springing di una nave possono essere molto
piccoli, la teoria fornisce le informazioni sulle forze eccitanti che
agiscono sulla nave nelle onde corte che producono tale fenomeno. Quindi,
quando queste forze si applicano alla nave come una semplice trave può essere
prevista la risposta vibratoria. Malgrado il fatto che la “strip theory” non
sia rigorosamente applicabile a tali onde corte, i risultati per una nave
d'alto mare sono stati trovati in buon accordo con le misure al vero. Se
le onde che eccitano lo springing fossero regolari, lo springing potrebbe
essere evitato da un piccolo cambiamento nella velocità. Ma in una rotta
reale che contiene una vasta gamma di frequenze lo springing varia in modo casuale
ed un cambio di velocità può avere scarso effetto. L'eccitazione e la
risposta dello springing possono allora essere trattate come i processi
stocastici che possono essere maneggiati mediante le tecniche già discusse.
Tuttavia, è stato studiato che le onde più lunghe nello spettro possono anche
eccitare la vibrazione dello scafo. Ciò introduce aspetti non lineari che
sono importanti da considerare rispetto alle risposte strutturali. Carichi di slamming Quando
una nave viaggia ad alte velocità, particolarmente in mari di prua, questa
può occasionalmente emergere da un'onda e rientrare nell'onda seguente con un
impatto gravoso o slam mentre il fondo entra in contatto con l'acqua. Altri
fenomeni sono associati all’impatto di grandi onde con le strutture di prua
costituite da pennoni o da masse d’acqua “green water” che invadono il ponte
ed impattano violentemente con le sovrastrutture esistenti. In ogni caso il
fenomeno consiste nell’impatto con un’alta velocità relativa fra la
superficie libera dell'acqua quasi incompressibile e una parte della
struttura della nave. Due
effetti notevoli possono essere causati dallo slamming del fondo. Ci possono
essere danni strutturali localizzati nella zona del fondo che ha sopportato
la più alta pressione di impatto. Ciò può includere lo sfondamento dei
fasciami o l’instabilità dei rinforzi interni, dei ponti e delle paratie. Un
secondo effetto dello slamming è una vibrazione transitoria dell’intero scafo
in cui il contributo principale viene dal modo di vibrare fondamentale
verticale con due nodi. Questa vibrazione indotta dallo slamming è chiamata
whipping e può provocare intensi sforzi di vibrazione uguali nel valore alle
sollecitazioni di flessione a bassa frequenza indotte dal moto ondoso. Si
veda la Figura 17 che mostra uno schema esemplificativo delle tensioni di
“whipping”.
Figura 17 Lo
slamming è possibile se queste due circostanze agiscono simultaneamente: -
il fondo di prua deve emergere dalla superficie delle onde. -
al momento del rientro la velocità relativa fra la parte inferiore della nave
e l'acqua deve eccedere un certo valore di soglia. Da esperimenti su modello,
la velocità della soglia è stata misurata prossima a 3.6 m/sec per navi da
carico. L'intensità
del whipping dipende dalla grandezza della forza che deriva dalla pressione
impulsiva dello slamming, sulla relativa posizione longitudinale e sulla
durata dell'impulso di tale forza. Gran parte delle informazioni disponibili
sull'intensità di pressione, p, derivante dallo slamming è stata ottenuta
dalle prove di modello. Questi sono stati effettuati con i modelli
bidimensionali in acqua tranquilla, con i modelli tridimensionali completi in
acqua tranquilla e con i modelli completi che si muovono nel moto ondoso. La
Figura 18. contiene una compilazione di tali dati di prova su modello.
Figura 18 Questi
risultati sono solitamente adattati ad una curva con una forma data da.
dove
v è la velocità verticale relativa. Il coefficiente k è indicato per tre tipi
di prove nella Figura 18. La pressione di impatto è distribuita sopra una
zona del fondo della nave nelle vicinanze immediate del punto di rientro ed è
tipicamente il massimo sulla linea centrale
in ogni istante di tempo. E’ stato trovato che le più alte pressioni
accadono dove il fondo è quasi piatto. La forza totale allora è data
dall’integrale di questa pressione sulla zona del fondo sulla quale agisce.
Poiché la prua della nave rientra in acqua, il punto di pressione massima
tende a muoversi verso la prua. Ad una data stazione sulla lunghezza, la
durata della pulsazione della pressione è tipicamente di pochi dieci
millisecondi, ma come conseguenza del movimento della posizione di rientro,
anche l’impulso di pressione si muove, mantenendo la sua intensità di picco.
La durata totale della forza d’impulso che la nave avverte sarà, quindi,
molte volte più grande della durata di impulso in un punto fisso. Questo
comportamento di spazio-tempo della forza è illustrato nella Figura 19.
Figura 19 Carichi inerziali sui
componenti Le
accelerazioni che derivano dai movimenti di una nave in una rotta producono
forze (o reazioni inerziali) sui componenti locali della nave, così come sul
personale, sul carico e sui liquidi nelle casse. Di conseguenza il calcolo
dei valori di queste forze sono spesso necessari per il progetto delle
strutture locali, delle fondazioni, delle legature, dei dispositivi di
fissaggio, ecc. Per tali scopi i valori massimi valutati di tali forze
possono usualmente essere considerati come carichi di progetto statici, a
causa dei periodi relativamente lunghi delle ampiezze dei movimenti della
nave. Le
vibrazioni dello scafo causate dalle macchine o dall’azione dell'elica
possono in alcuni casi causare risposte in risonanza dei componenti
strutturali. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ingegnerianavale.net -
Tutti i Diritti Riservati |